Created on 2013-01-31 23:14:00
The Fourier transform has the effect of connecting the end of the FFT record to its beginning, forming an endless loop of data in the calculation.
In almost all cases, there is a discontinuity at the “splice,” and just like a bad audio edit, the discontinuity is an impulse that spills energy across the spectrum. Unmodified, this energy swamps the useful data. Two techniques are employed to eliminate the discontinuity: FFT windowing, and the use of synchronous FFTs.
An FFT window is an amplitude envelope that is applied to the FFT record before the transform. FFT windows change the data, and therefore affect the results. However, a number of windows have been developed that provide useful results while eliminating the looping discontinuity.
The example below shows the Hann window in the time domain, with the FFT record at the top, the window function in the center and the modified FFT record at the bottom. Other window functions have different shapes to optimize the resultant FFT for different purposes. What they all have in common is a tapering to zero at both ends, to eliminate the discontinuity.
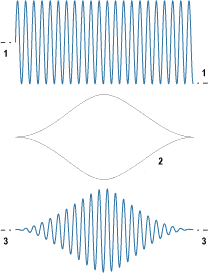
The windows provided with APx500 are detailed here:
Hann
The Hann window is a raised cosine window that provides good selectivity near the top of the main lobe (about –6 dB at one bin away from center and about –30 dB at two bins away), with no side lobes. Its skirts more than 3 bins off center are not as steep as the Blackman-Harris window. The Hann window causes approximately –1.5 dB maximum amplitude error due to window attenuation, if the signal is at the extreme edge of the bin.
Blackman-Harris 3-term
The Blackman-Harris 3-term window is about –5 dB in the bins adjacent to the center, about –20 dB two bins off, and about –160 dB three bins off. Response fall-off is monotonic. Scallop loss is 1.1 dB maximum.
Blackman-Harris 4-term
The Blackman-Harris 4-term window is a minimum side lobe window, as found in Audio Precision AP2700 software. When compared to the Hann window, it is not quite as selective across the central several bins (about –3 dB in the adjacent bins and about –14 dB at two bins off), but has steeper skirts beyond that point. The Blackman-Harris window has side lobes below –92 dB (response fall-off is not monotonic). It has a reasonably flat top with a maximum amplitude error of about –0.8 dB if the signal is at the extreme edge of the bin.
Flat Top
The Flat-Top window is designed for the greatest amplitude measurement accuracy. It provides a maximum amplitude error due to window attenuation of less than –0.02 dB. However, its selectivity is poorer than the other windows. The Flat-Top window is the appropriate window for accurate amplitude measurements (such as when measuring individual harmonics) except when signals are so closely spaced that its selectivity becomes a problem.
AP-Equiripple (the default)
The Equiripple window, developed at Audio Precision, is an approximation to the Dolph-Chebyshev window that has the narrowest main lobe width for a given maximum side lobe depth. The main lobe is approximately 12 bins wide; that is, the first null is about six bins from the main lobe center. The first side lobe, which is also the highest, is –147 dB from the main lobe. The maximum amplitude error with a signal at the bin boundary is about 0.5dB.