THD and THD+N – Similar, but not the same
THD and THD+N are acronyms for Total Harmonic Distortion and Total Harmonic Distortion Plus Noise. Both are measures of harmonic distortion – the degree to which a device alters a pure sinusoidal signal by adding harmonics to the fundamental signal. They are closely related, but there’s an important difference between them that is often overlooked. In fact, the term THD is often used incorrectly in place of THD+N in publications and specification documents.
Audio Distortion
The primary job of any audio device is to faithfully reproduce or transmit the audio signal that is input to it. An ideal, linear audio device will produce an output signal that is an identical scaled version of its input signal. Anything that alters the input signal in any way, other than changing its magnitude, is known as distortion.
A classic means of detecting audio signal distortion is to stimulate a device under test (DUT) with a pure sine wave and then conduct a spectral analysis of the DUT output. Sine waves are used because a pure sine signal has the unique property that all its energy is concentrated at a single point in the frequency spectrum. This makes it easy to analyze the output from the DUT for unwanted distortion components. When a single sine wave is used as the stimulus, nonlinearities in the DUT cause harmonic distortion, wherein distortion components occur at harmonics (integer multiples of the sine signal’s frequency, or fundamental frequency).
Total Harmonic Distortion Plus Noise
The THD+N technique is the most common method of measuring harmonic distortion. In its basic form, it is implemented with a sharp notch filter tuned to the fundamental sine frequency, a bandwidth limiting filter, and an rms level meter (Figure 1). The notch filter and bandwidth limiting filter can also be realized with FFT analysis. The notch filter removes the fundamental sine signal, leaving a residual signal which consists of the harmonics and noise. The THD+N Ratio is calculated as the bandwidth limited rms level of the residual divided by the rms level of the entire signal.

Figure 1. Block diagram of a THD+N analyzer.
THD+N ratio is usually expressed either in percent or dB. Percent is commonly used for THD+N levels of 0.01% or higher. For very low distortion, dB units are easier to work with. For example, the typical residual distortion of an APx555 audio analyzer’s analog I/O (Figure 2) is -120 dB or 0.0001%.
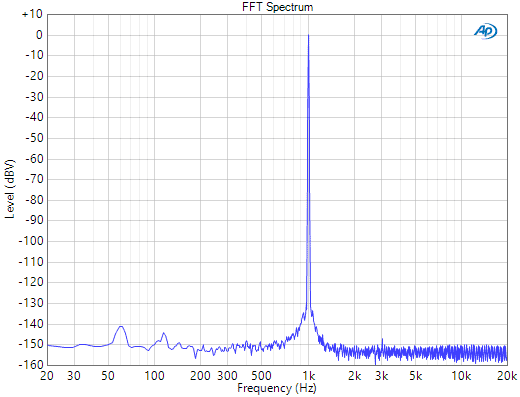
Figure 2. FFT of a stimulus signal from the APx555 (High Performance Sine Generator, 1 Vrms sine at 1 kHz
Sometimes a weighting filter is applied to the residual, which will lower the measured THD+N ratio. For example, an A-weighting filter might be used to hide the presence of hum artifacts at multiples of the AC mains voltage frequency (50 or 60 Hz). If a weighting filter is used, this should be clearly stated with the reported THD+N result.
Conceptually, the THD+N measurement technique is appealing because anything in the DUT output signal beside the pure stimulus signal will degrade the measurement result. A low THD+N result indicates not only that harmonic distortion is low, but also that hum, interference signals and broadband noise introduced by the DUT are at or below the low measured value.
When THD+N measurements results are stated or specified, to be meaningful, details such as the stimulus level and frequency (or frequency range), the measurement bandwidth and the DUT gain, should be included. For example:
Correct: THD+N less than 0.01%, 1 Vrms, 20 Hz - 20 kHz, unity gain, 20 kHz BW
Incorrect: THD less than 0.01%
Total Harmonic Distortion
A THD measurement is similar to a THD+N measurement, except that the analysis considers only the harmonic distortion components and ignores everything else. Hence, the test setup is inherently more complicated than the THD+N technique. In the early days of audio test, this would require an analyzer with a tunable narrow bandpass filter, that could be tuned to each harmonic in serial fashion. Currently, THD is derived from FFT spectrum analysis (Figure 3, below).
Knowing the relative strength of harmonic components can be a useful design tool, since different non-linearity mechanisms can give rise to different patterns of harmonic distribution (odd versus even numbered harmonics, etc.). The THD+N measurement in APx has a convenient feature that clearly displays the fundamental and the first 10 harmonics in a result called the Distortion Product Ratio (Figure 4, below), while simultaneously measuring both THD+N and THD.
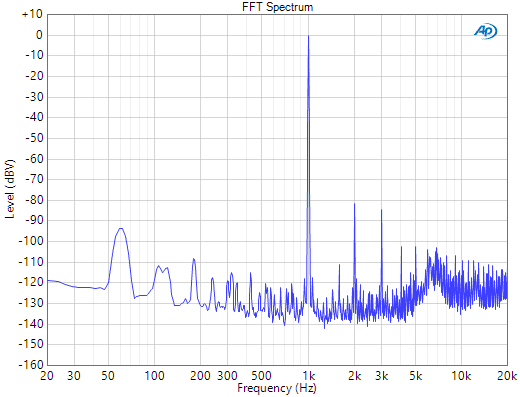
Figure 3. FFT of DUT output signal (APx1701, 20 dB gain, 8-ohm load).
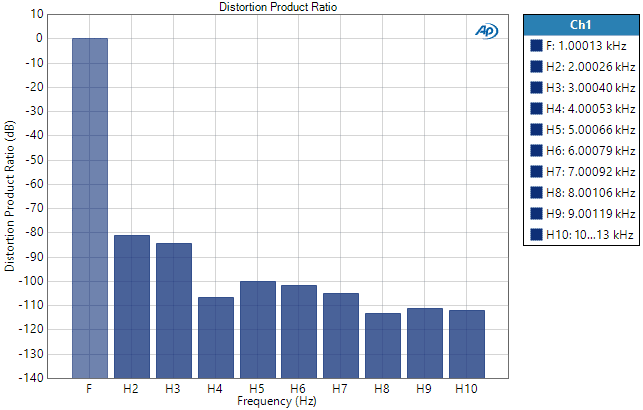
Figure 4. Distortion Product Ratio (right) of DUT output signal (APx1701, 20 dB gain, 8-ohm load).
The THD Ratio is calculated as the RSS summation (square root of the sum of squares) of the harmonic components divided by the rms level of the fundamental signal. Like THD+N, it is typically expressed in percent or dB.
As noted above, many publications incorrectly use the term THD when referring to a THD+N test (even the recently published IEC standard on audio amplifiers does so). It’s important to make the distinction between the two, because the THD ratio will always be less than the THD+N ratio.
Note that the number of harmonics included in the analysis is important, and the analysis bandwidth of the audio analyzer comes into play in this regard. For example, if the input bandwidth is, say 22 kHz, the third harmonic of the signal will only be included up to fundamental frequencies of about 7 kHz and the second harmonic up to about 11 kHz.
When THD results are reported, the same measurement details as THD+N should be included, except that the number of harmonics included replaces the measurement bandwidth. For example:
Correct: THD (through 6th harmonic) less than 0.01%, 1 Vrms, 20 Hz - 20 kHz, unity gain
Incorrect: THD less than 0.01%
THD Usage and Definitions
THD is preferred over THD+N for applications involving loudspeakers and microphones, no doubt due to the relatively high levels of ambient noise that are typically present when making acoustic measurements.
There are two slightly different definitions of THD ratio, sometimes referred to as the IEC method and the IEEE method. In the IEC method, THD is calculated as the RSS summation of 2nd through nth harmonics divided by the rms level of the total signal (fundamental plus harmonics plus noise). This is shown in equation (1), where Hi represents the level of the ith harmonic and ST represents the rms level of the total signal.
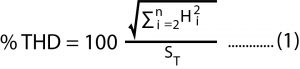
The IEEE method (equation 2) is similar, except that the RSS summation of harmonics is divided by the rms level of the fundamental signal instead of the rms level of the total signal.
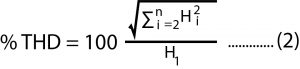
For the low levels of distortion present in most audio systems, there is very little difference between the two methods. In the APx500 software, the IEC method is used in measurements based on classic sine wave testing such as the THD+N measurement and Stepped Frequency Sweep. However, due to the nature of the signal processing involved, the IEEE method is used in measurements based on the log-swept sine chirp (Continuous Sweep and Acoustic Response).
SINAD
An acronym for Signal to Noise and Distortion ratio, SINAD is a measure of harmonic distortion and noise that was originally used in testing FM radio tuners, and is favored in the communication industry. It is measured in the same way as THD+N, and in fact, in this context, it is simply the inverse of the THD+N ratio. For example, a THD+N ratio of 0.1% (-60 dB) is equivalent to SINAD = +60 dB.
SINAD is also used to quantify noise and distortion in analog to digital converters (ADCs), and in this context, it has a more specific definition: SINAD in ADCs is calculated from FFT analysis and includes all FFT bins except the DC bin up to the Nyquist frequency (one half the sample rate). As a result, with this definition of SINAD, it is only equivalent to THD+N if the residual is analyzed over exactly this same bandwidth.